In this post I am going to share my thoughts about the education and some of the current educational approaches. I was provoked by an article by I. V. Arnold published in the Russian magazine Математическое просвещение year 1936, issue #8.
The article was about choosing a winning strategy for the following game (I don’t know the name of the game so if you know it please drop a comment; I think the game origin is from Japan or China). Here is the game: there are two players and two heaps of objects. Let’s call them player A, player B, heap A (contains a>0 objects) and heap B (contains b>0 objects) respectively. Each player takes a turn and removes objects from the heaps according the following rules:
- at least one object should be removed
- a player may remove any number of objects from either heap A or heap B
- a player may remove equal number of objects from both heap A and heap B
Player A makes the first turn and the player who takes the last object(s) wins the game. Knowing the numbers a and b you should decide whether to start the game as a player A or to offer the first turn to your opponent.
Sometimes this game is given as a problem in mathematical competitions (or less rare in informatics ones). When I was at school we studied this game in math class. Back then I was taught a geometric based approach that chooses a winning strategy. I will skim the solution here without going in much details because this is not the purpose of the post.
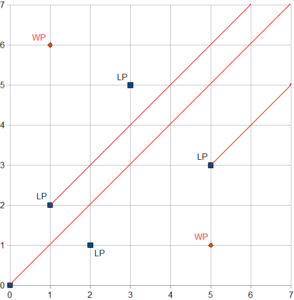
As the game state is defined by the numbers a and b we can naturally denote it with the ordered pair (a, b). Then we can naturally present the game state on a coordinate system. Let’s say a=2, b=1 so we have (2, 1) point on the coordinate system and let’s put a pawn on this point.
According the rules we may move the pawn left, down and diagonally towards (0, 0) point. It’s easy to see that it is not possible to win the game if we start from position (2, 1) so let’s define position (2, 1) as a loosing position (LP). I am going to provide the list of all possible moves:
- (2, 1) → (2, 0). The next move (2, 0) → (0, 0) wins the game
- (2, 1) → (1, 1). The next move (1, 1) → (0, 0) wins the game
- (2, 1) → (0, 1). The next move (0, 1) → (0, 0) wins the game
- (2, 1) → (1, 0). The next move (1, 0) → (0, 0) wins the game
Point (0, 0) should be also considered as a loosing position. We notice that if (a, b) is a loosing position then (b, a) is also a loosing position. To find the next loosing position we have to draw all horizontal, vertical and diagonal lines from all existing loosing points and find the first point not laying on those lines.
Using this approach we see (5, 3) is a loosing position while (5, 1) is a winning position (WP). The strategy is already obvious – if the starting position is LP we should offer the first turn to our opponent, otherwise we should start the game and move the pawn to a loosing position.
So I was given an algorithm/recipe how to play and win the game. Back then my teacher said that the game is related to the Fibonacci numbers but she did not provide additional information. It wasn’t until I read the article mentioned above and I’ve finally understood the relation between the game and the Fibonacci number (and the golden ratio in particular).
Back to the main topic of this post. 20 years ago my teacher taught me how to solve particular math problem. I was given an algorithm/recipe that explains the winning game strategy. Indeed it is true that I didn’t know why exactly the algorithm works but still it was presented in a very simple and efficient way. In fact I knew it for the last 20 years. This triggered some thoughts about here-is-the-recipe kind of eduction.
It seems that here-is-the-recipe kind of education works pretty well. My experience tells me so. Most of the time I’ve worked in a team and I had plenty of chances to ask my colleagues about things in their expertise. Sometimes I was given an explanatory answer but most of the time I was given a sort of this-is-the-way-things-are-done answer. And it works. So I believe that here-is-the-recipe kind of education is the proper one for many domains. Not surprisingly these domains are well established, people have already got the know-how and structure it. Let me provide some examples.
One example are design patterns. Once a problem is recognized as a pattern a solution is applied. Usually applying the solution does not require much understanding and can be done by almost everyone. Sometimes applying the solution requires further analysis and the if not done properly the result could be messy. This is very well realized by the authors of AntiPatterns: Refactoring Software, Architectures, and Projects in Crisis. They talk about 1980’s when there were a lack of talented architects and a disability of the academic community to provide detailed knowledge in problem solving. I think that nowadays the situation is not much different. One thing for sure – today the IT is more dynamic than ever. Big companies rule the market. They usually release new technologies every 18-24 months. Many small companies play on the scene as well. They (re)act much faster. Some technologies fail, some succeed. It is much like Darwin’s natural selection. The academic education can not respond properly. Fortunately today’s question-and-answer community web sites fill that gap especially for the most common problems.
Another example are the modern frameworks and components. I’ve seen many people using them successfully without much understanding the foundations. Actually this is arguable because one of the features of a good framework/component is that one can use it without knowing how it works. Of course sometimes it is not that easy. Sometimes using a framework requires a change in the mind set of the developer and it takes some time. In such cases the question-and-answer community web sites often recommend not the best (sometimes even bad) practices. I guess it all depends on the speed of adopting the framework. If many people embrace the new framework/technology the best practices are established much faster.
On the other side sometimes here-is-the-recipe kind of education does not work. As far as can I tell this happens for two major reasons.
The first one is when a technology/framework is replaced by a newer one. It could be because it is too complex and/or it contains design flaws or whatever. One such example is COM. I remember two books by Don Box: Essential COM (1998) and Essential .NET (2002). The first one opens with “COM as a Better C++” while the second one opens with “The CLR as a Better COM”. Back then the times were different and four years were not a long period. Although COM was introduced in 1993 the know-how about it was not well structured.
The second reason is when the domain is too specific and/or too rapidly changing. In case of too specific domain there is not enough public know-how. The best practices usually are not established at all. In case of rapidly changing domain even if there is a know-how there is not enough time to structured it.
Of course no teaching/education methodology is perfect. So far I think the existing ones do their job as expected. Though there is a lot of space for improvement. Recently I met a schoolmate of mine who is a high school Informatics teacher. We had an interesting discussion on this topic and I will share it in another post. Stay tuned.